Topological Sorting
Think back to when you were in college.
You declared your major in Graph Theory, and you were given a list required classes that you must take. Some of those classes had prerequisites. Therefore, there is a certain order in which you had to take the classes. As Graph Theory major, your first thought will be to immediately put all your required classes in a directed acyclic graph and perform a topological sort to determine when you will take each class.
Directed Acyclic Graph
For all those who did not major in graph theory, you might be wondering— what's a directed acyclic graph?
A directed acyclic graph is a special kind of graph, which typically represents a series of activities performed in a given order. In this type of graph, each relationship has a defined direction— thus the directed in directed acyclic graphs — and there is no loops or cycles in the graph — thus the acyclic.
That means that if you follow the relationships that connect one node to another, there is no path back to the initial node. Here is an example of what this might look like:
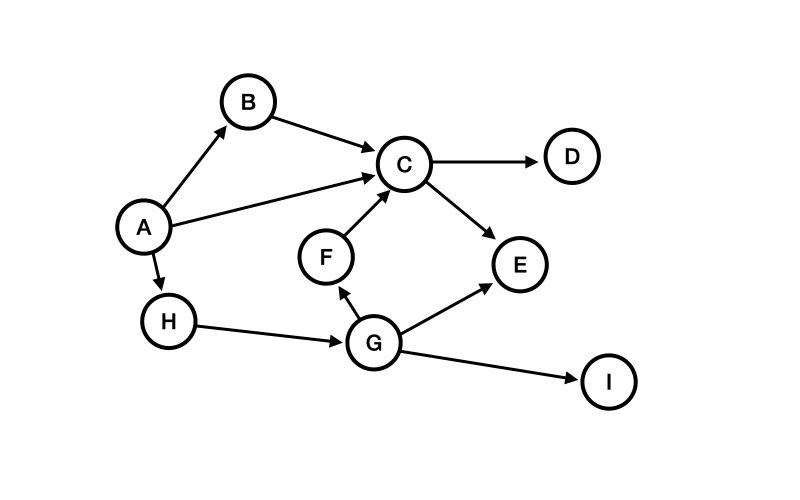
Topological Sort
When we perform a topological sort (or top sort for short), we are trying to find a given order for the nodes in our graph. Another way of thinking about this is that: topological sorting means you could put all the nodes in a line and all the edges would point to the right. Below is a sorted directed acyclic graph:
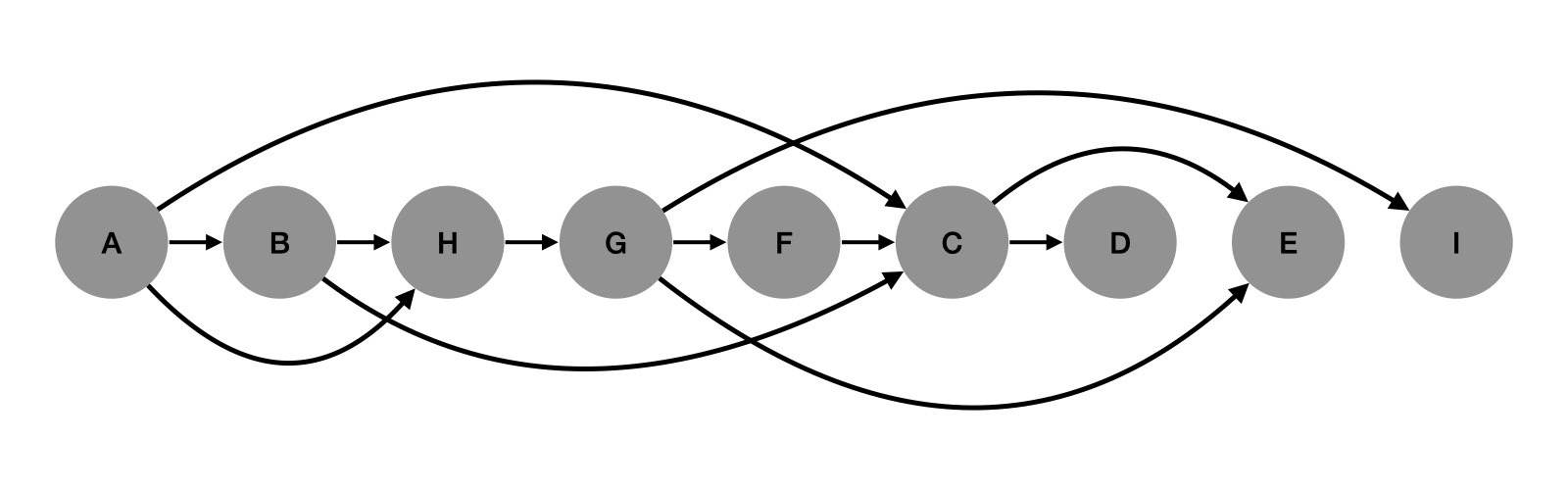
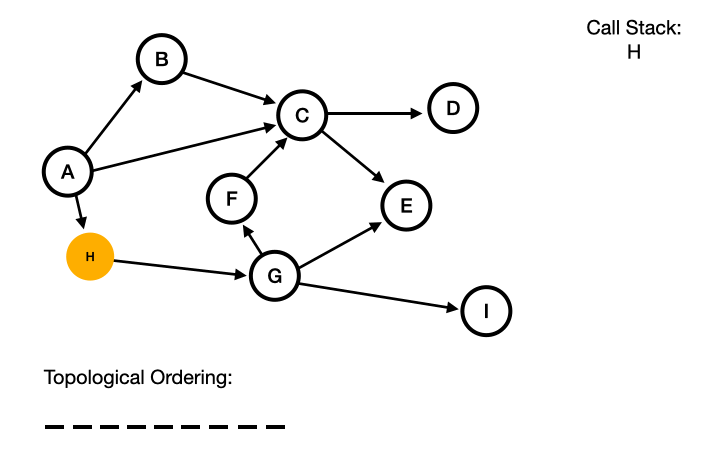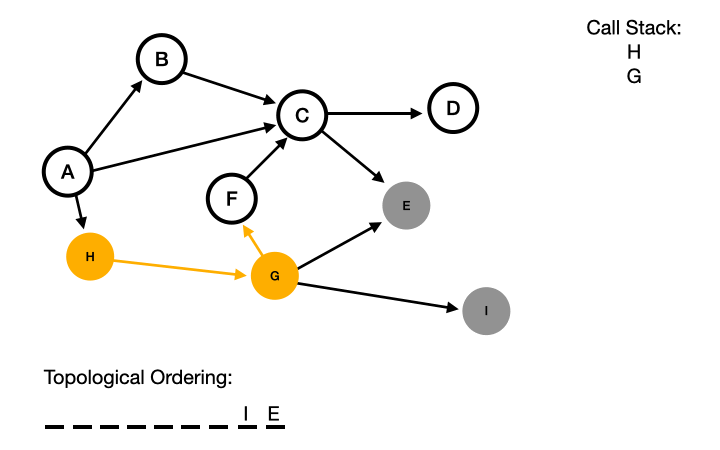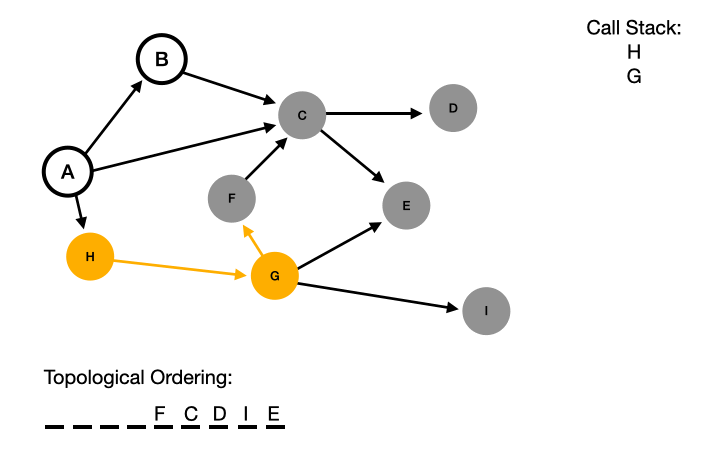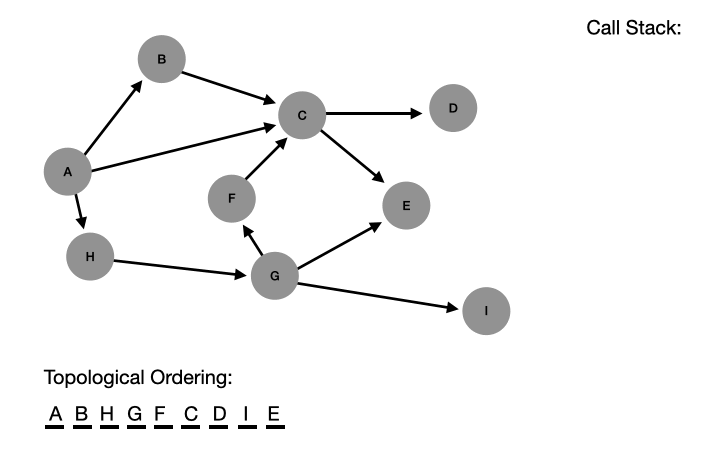
As we will see, this doesn't necessarily mean that there is one canonical order in which to sort the nodes. There can be many different orders. But as long as all the relationships point in the same direction, it has been successfully sorted.
Let's think about why this type of graph is needed for a topological sort. If you had nodes with undirected relationships, when you go to order those two nodes, you wouldn't be able to determine which one should come first. And the same is true for graphs with loops.
Imagine you had if "Intro to Graphs" course that required "Intro to Cypher" but that "Intro to Cypher" course required "Intro to Graphs" as prerequisite. What sort of terrible kafkaesque school would that be?
The Algorithm
Top sort will sort all of the nodes in your graph or subgraph. As with most algorithms, we will perform a set of steps on a loop until exhaustion. So let's get started.
First, we pick a random node in the graph or subgraph. In this case H:
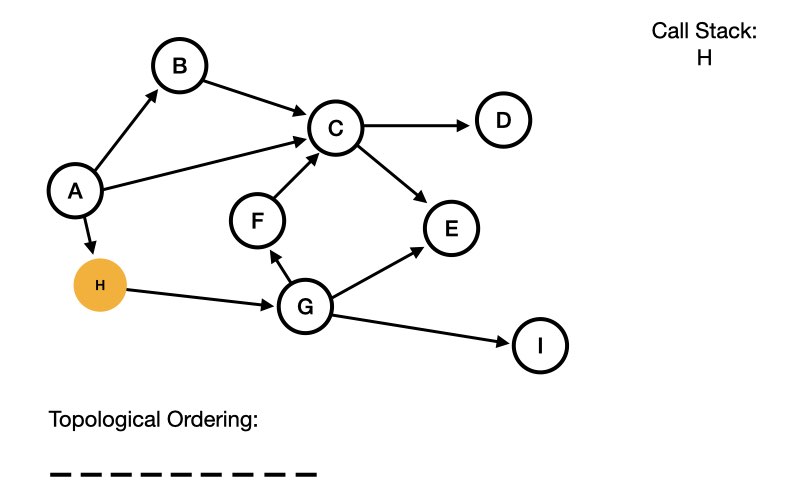
Then we perform a depth first search, adding each node to our call stack as we go, until we can no longer go any further.
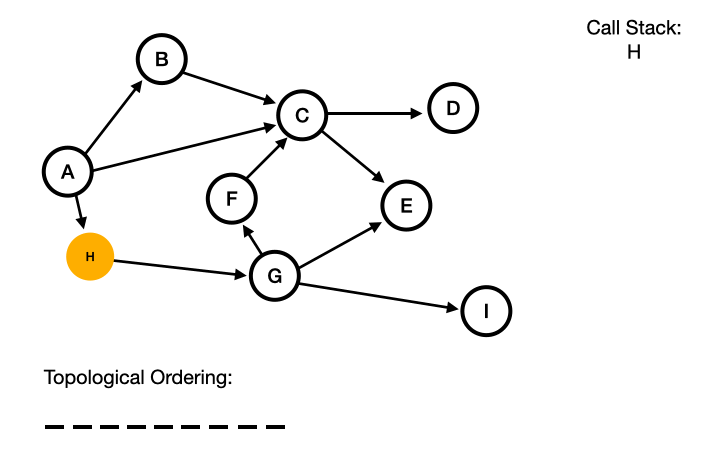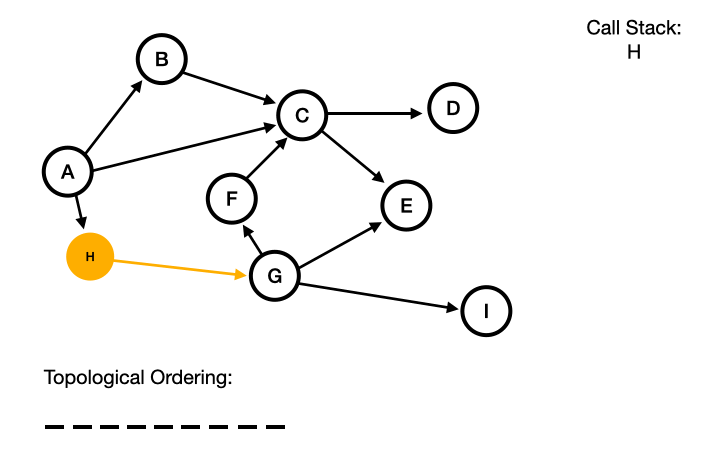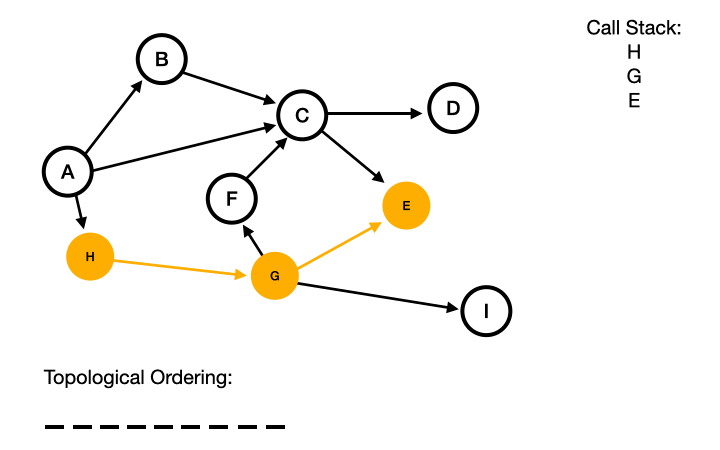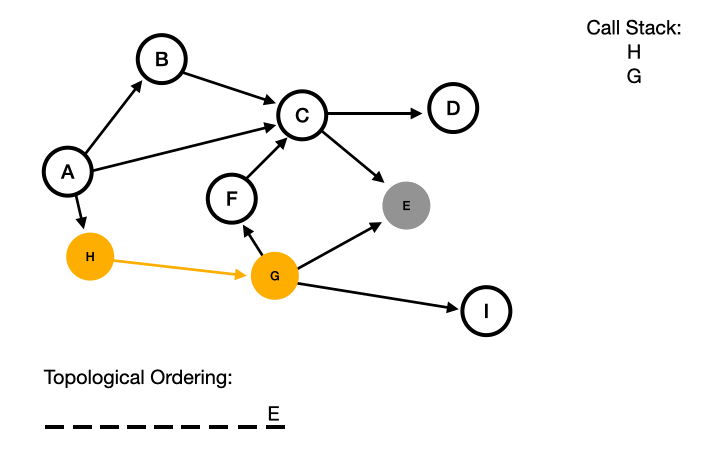
At this point, we end on Node E. We then pop this off our call stack and put it at the end of our topological ordering.
Now the recursion.
We go back to Node G and continue our depth first search. This time excluding Node E since we have already visited it. Instead, we go to Node I, which is also a dead end. So we will pop that off the call stack as well and add it to our topological ordering.
You may be wondering why we didn't go to Node F at this point. And you are right we could have gone to Node F. This is why topological ordering does not have one given order. Rather it gives you one possible order.
Let's watch how the algorithm sorts through this graph in full.
Limitations
Another important limitation is that this sorts the entire graph. Think about if our course requirements example. This graph could potentially include required course in majors that you are not taking. So how would you exclude those courses?
You would have to take a subgraph. One method would be to do some form of dependency filtering before performing a top sort. So for example, if you just wanted to know what nodes E depends on, you could do a reverse depth first search to create a subgraph and then perform a top sort on that. This would exclude Nodes D and I.
So there you have it! A quick and easy way to see when you should take what classes! And you didn't even need to go to college to learn how to do that!