PageRank
Imagine we have the following graph:
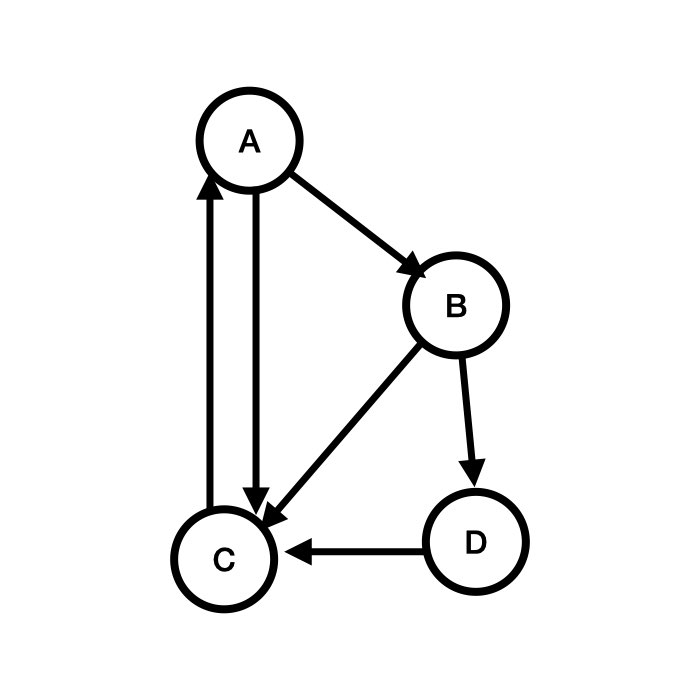
What do you think are the most important nodes? Maybe C and A? Node C is linked to the most out of all the nodes, so it is easy to see why it would be considered important.
Whereas Node A is linked to by the most important Node so perhaps it is just a little more important than Nodes B and D.
PageRank puts this intuition into practice. It determines centrality based on the quality and quantity of the incoming relationships to a given node.
The most famous use of this algorithm is to determine what webpages are most important. We can imagine each node in our graph as a webpage and each relationship as a hyperlink between those pages. Some pages will link to eachother but some will only have outbound links.
PageRank— named after Larry Page, cofounder of Google, not webpages — considers a few things in determining the quality of incoming links.
- Pages with many outbound links are considered less valuable
- Pages with many inbound links are considered more valuable
- There needs to be damping factor to account for users directly entering an address rather than clicking on a link, otherwise, the formula could go on forever
The formula
Ugh. We are gonna have to write out a formula for this one. But I will try and keep it simple.
Let's break this monster down. First the damping factor, which is represented by the d. Imagine you are randomly surfing the web. You go on your favorite sports website and click on different article on that site, back to sites homepage, to new articles, but then at some point, you enter a new website directly without clicking a hyperlink.
That process of exiting the website entirely is the damping. Typically, we use 85% as the damping factor. Meaning that 85% of the time, you click hyperlinks rather than enter a new address.
Here is how we use the damping factor
I don't think we need to go through exactly what we are doing with this but suffice it to say, it is used to modulate the combined scores of all the inbound linking pages. The real important bit is how we sum of the scores of the inbound links.
For each inbound link, we divide the current page rank by the number of outbound links and then sum it all together to get the new page rank for that page.
Iterations
As you might suspect, we don't just do this once but we do it a bunch of times until the values converge or until a maximum number of iterations is reached.
Let's walk through it once to see what happens. Initially, we assume that all pages are ranked evenly so:
- Page A is 1/4 of all the pages or .25
- Page B is 1/4 or .25
- Page C is 1/4 or .25
- Page D is 1/4 or .25
Then we run our formula for each page.
For Page A
Only Page C links to Page A so the filling in the formula will look like the following:
or
For Page B
In this case, Only Page A links to Page B, but because Page A links to two different pages, each link is a little less valuable.
or
For Page C
Page C is linked to by all the other pages, so we might guess that it is going to be the most important.
or
Here we can see how important it is to be linked to by multiple pages but also that Page D's link is more important because it only links to C.
For Page D
Page D is only linked to by Page B so it will mirror what we saw with Page B, which is similarly connected.
In this case, Only Page A links to Page B, but because Page A links to two different pages, each link is a little less valuable.
or
Ok so now we have gone through one iteration and our new page ranks are as follows:
- Page A = 0.25
- Page B = 0.14375
- Page C = 0.4625
- Page D = 0.14375
We could then run this iteration again and again until a convergence is met. We could decide that it has converged when the changed PageRanks between iterations don't change all that much or fall below a predefined level.
Strengths and Weaknesses
This doesn't have to be all about linking websites. This can apply to many different domains. The best things about PageRank is that it considers the quality of the linking nodes rather than just the fact that the node links at all.
It also works well with directed graphs, acknowledging that the relationships between nodes are oftentimes one way.
There are so cases when PageRank will not work as well. Older nodes will be more valuable as they have more time to develop connections. And nodes that have no outgoing links (called sink nodes) can disrupt the flow of rank.
The original PageRank is unweighted meaning that the quality of the relationships do not impact the rank.