Louvain

At this point, we have a good understanding of what modularity is, but now we need to find a good way to optimize it. Enter Louvain.

Take a look at the below graph.

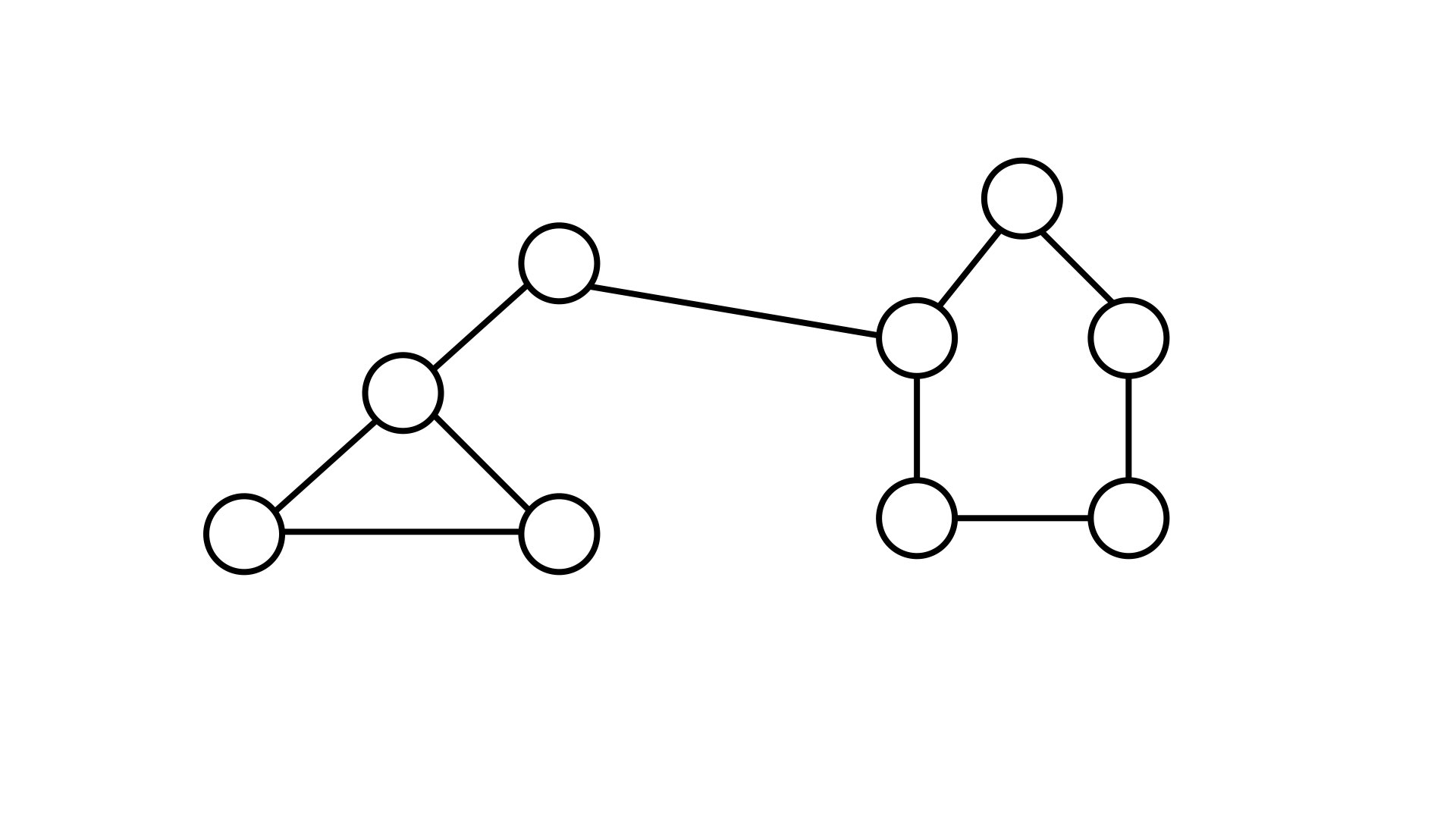
As usual, we can spot what we would imagine the two partitions to be. But how can we formalize our logic so that we can repeat it at scale?

Louvain works in two phases: local modularity optimization and then community aggregation. These two steps loop through each other until there are no more gains in modularity.

Phase I: Modularity Optimization

Initially, Louvain each node belongs in its own cluster— called singleton communities.

For each node, we remove it from its current community and add it to the community of one of its neighbors where the gain in modularity is at its greatest. This makes Louvain a greedy algorithm as we are trying to optmize the locally optimal choice.

We repeat this process until no nodes move from their current choice.

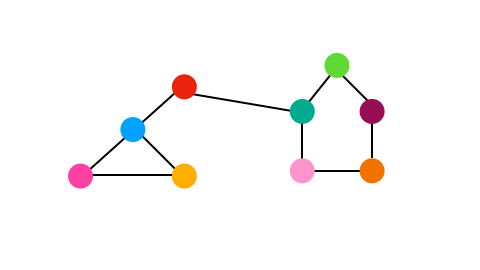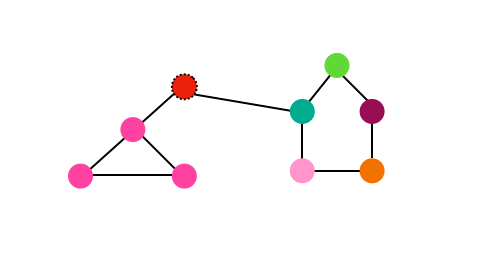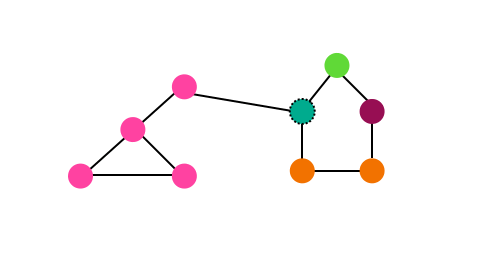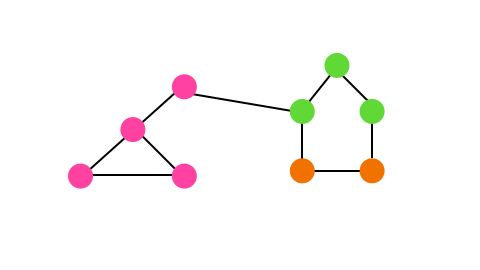
Phase II: Community Aggregation

Next we treat all nodes within a community as one big node. So practically, what does this look like.

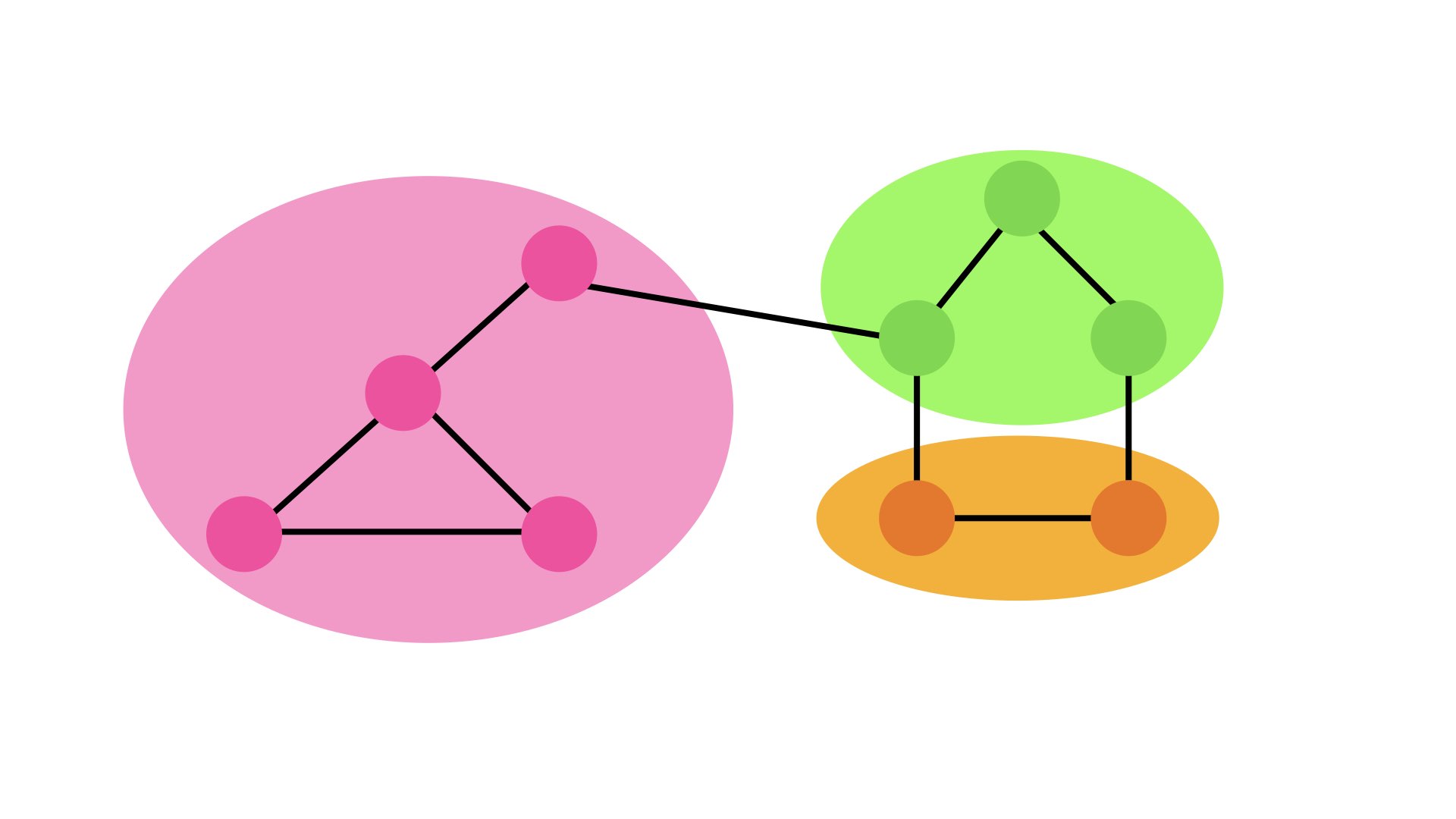
Relationships within communities are counted as self loops and edges between communities are merged together and their weights are added.

There is some tricky math stuff going on here to ensure that the current modularity score is maintained throughout this transformation that we will not dive into, but know in your heart of hearts that it is happening.

Louvain then tries to optimize our new nodes into communities. And in our example, it looks like it merges two communities.

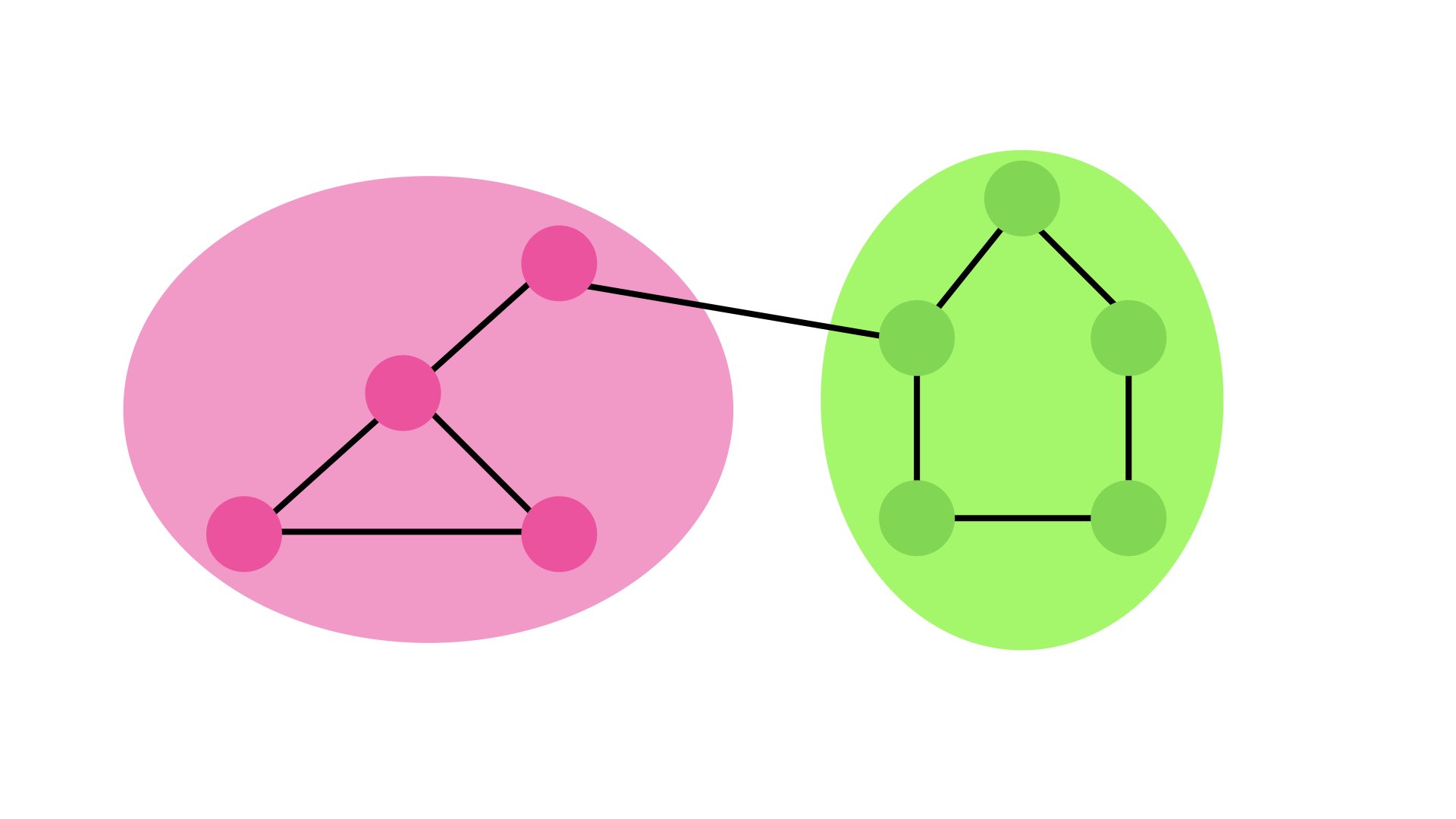
It will keep attempting this loop of local modularity optimization and community aggregation until there is no more gains in modularity.

And voila! We have, at least a locally optimized, set of communities! Huge Success!