Link Prediction
Something that I have always wondered as I have gotten older and more into graph theory is: how do we make new friends?
Not on a personal level, but how do make new friends between different nodes in a graph.
This is the fundamental question behind link prediction. If we have two nodes in a graph that do not currently have a link, should they? Would they be good friends? When you are on a social media site and see recommended followers or connections, you are likely looking at the results of a link prediction algorithm.
The applications for this are very reaching. Essentially any recommendation engine could be powered by link prediction, though there are often other algos that can provide better recommendations.
Common Neighbors
Consider the below graph of friends:
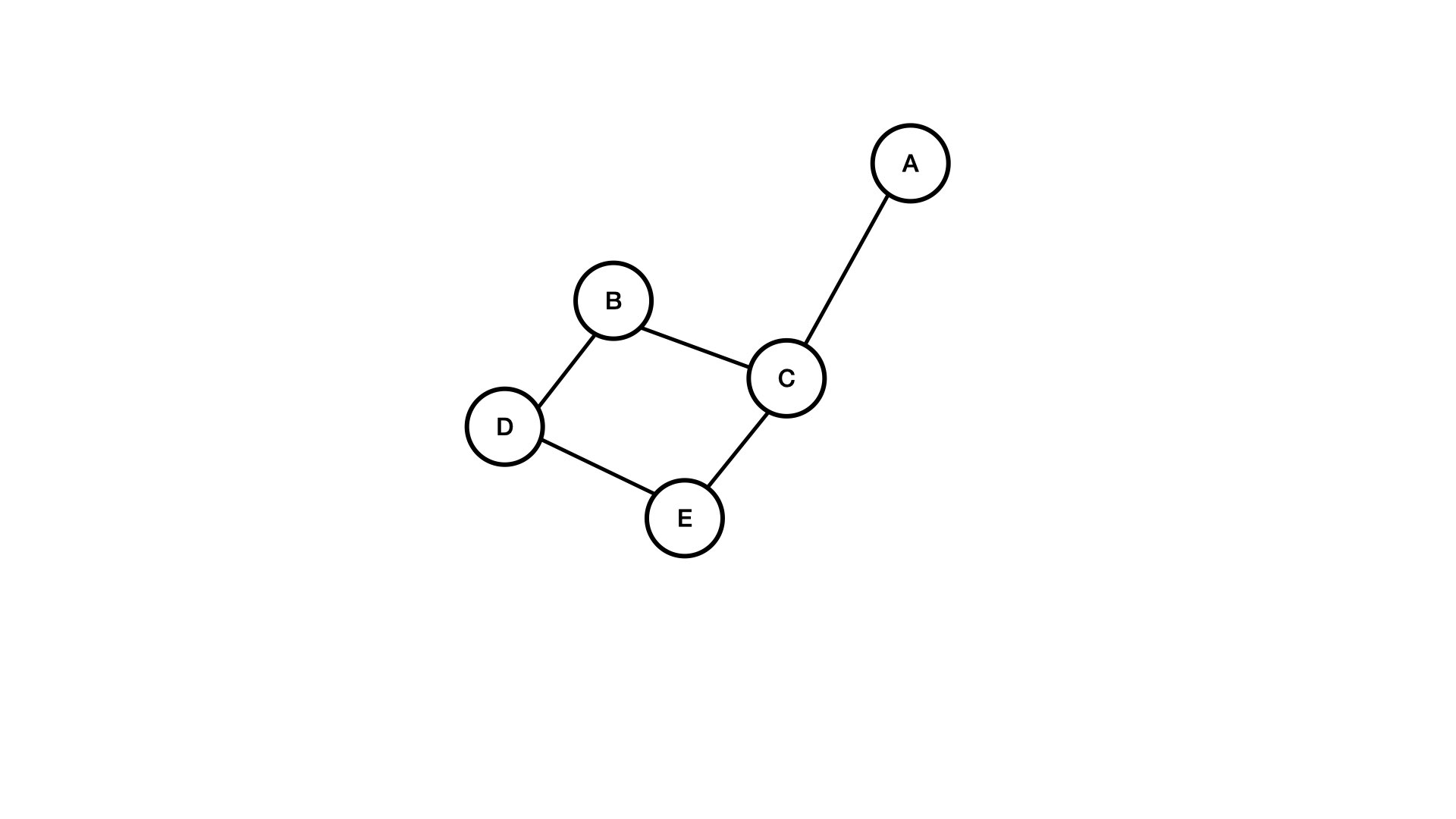
I think intuitively we can figure out where potential missing links could be. And even how we would describe as the most egregious missing links is pretty obvious as well. Nodes who have lots of friends in common with other nodes might make sense to suggest as friends.
We can even express that simply as so:
Basically, what this formula is doing is for Nodes A & B give me the total number of nodes they have in common. For A & B, this equates to:
Ok that is pretty simple, these two nodes only have one neighbor in common— C. But we aren't doing too much — or really anything at all — to measure the quality of the relationships.
Jaccard Coefficient
So what do we mean by quality relationships. I think the Shakira example explains this best. On Instagram, if you follow Shakira, how likely are you to be friends with one of her followers?
There is almost no chance. She's just too popular.
So we need someway to modulate the value of Shakira. Something to contain it. Most the below formulas will be working on this principle, but let's start with the simplest— the Jaccard Coefficient:
So what are we looking at here. In the nominator, we have our common neighbors algorithm, where we find the intersection of all the nodes in common between A and B. And in the denominator, we have just the opposite. We have all the nodes that come off A and B regardless of if they are in common.
As we can see, because Node C has a couple of nodes coming off of it, its prediction power is somewhat limited. This is a small graph, but you can imagine how much the predictive power of someone with millions of nodes would be diluted.
Resource Allocation
What if we thought of predictive power as a finite resource that is spread evenly between nodes. Imagine predictive power as a gallon of water and each relationship as a pipe. When you pour water into a node, it will flow evenly through each relationship/pipe to the adjoining nodes.
The more relationships attached to a node, the less "water" can get to adjoining pipe.
That's the intuition behind resource allocation, which can be expressed mathematically as
Note: I am overly annotating these formulas for readability
So what are we talking about here. Basically, for every common neighbor of A and B, we are going to multiply it by one over the degree of that common neighbor. So for our A and B example, we only have one common neighbor— C, which has a degree of three.
It is easy to see how our water analogy works here. A sink with three drains would only have 1/3 of water pour down any given drain.
The Adamic-Adar algorithm is a further refinement of this concept, but instead of taking 1 over the degree of Z, it takes 1 over the log of the degree of z.
Preferential Attachment
We have made a lot of noise about how nodes with too many relationships may not be predictive for link prediction. But sometimes the exact opposite is true. Sometimes nodes with a high degree are more active in a network and thus are more likely to form new attachments in the future.
The formula for this is dead simple.
Basically, multiply the number of neighbors of A times the number of neighbors of B, which in our case would look like