Dijkstra's Algorithm

Over a cup of coffee in 1956, the young dutch mathematician devised one of the most famous formulas in graph— Dijkstra's algorithm. He was chatting with his then fiancee about what would be the shortest path between Rotterdam and Groningen in an Amsterdam cafe. How lovely and how dutch.

So what did he come up with?

Setting the Stage

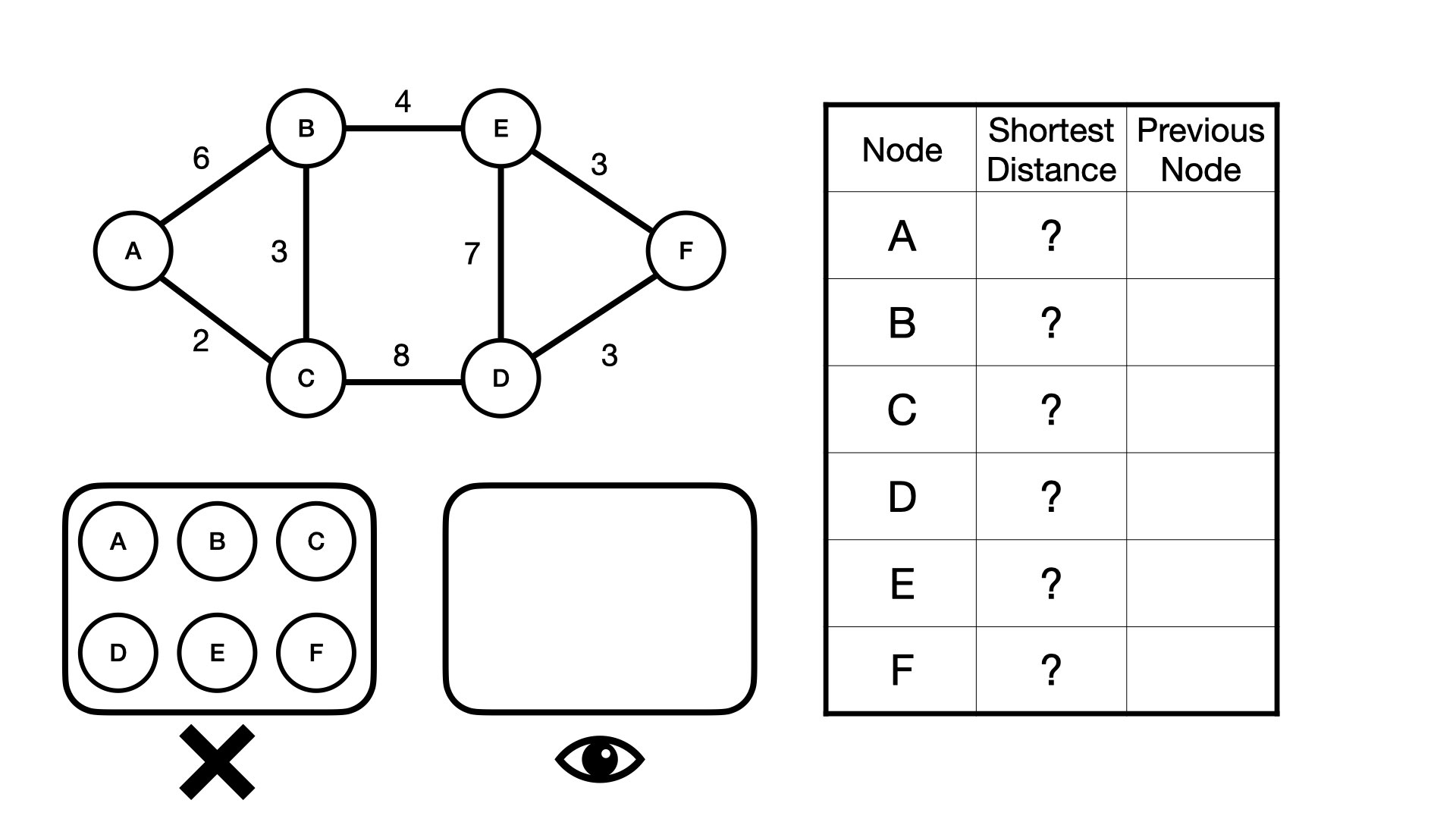
Let's imagine a set of nodes— these could be cities, subway stops, stores, whatever— and lines connecting them. In our example, we are interested in finding the shortest path between "A" and "F".

In reality, our algorithm will calculate the distance between A and all other nodes, rather than just the shortest distance between A and F. In fact, what our algorithm will do is track and update the shortest distance between A and a given node over the course of multiple iterations.

It does this by keeping track of a few things.

• What nodes have been visited and what nodes have not been visited
• The current shortest distance between the starting node and the node of interest
• And the previous node that leads us to the current shortest distance

Inside the Caves

Imagine this. You are trapped in deep in an old mine at the bottom of a cave. You have a map to get out detailing all the different tunnels and how to get to the exit. You want to find the quickest way to get out.

Let's imagine each node in our graph as a chamber cave in the mine. We stuck in Cave A and are trying to get to Cave F, which has an elevator out.

You could simply walk out but that would be too reasonable. Instead, you want to quickly figure out the fastest way to walk out.

What dijkstra's algorithm does is it calculates the current shortest distance from Cave A to all other caves by iterating through "unvisited" caves.

Iterate through

You have to give Dijkstra a starting node, which in our case is Cave A.

We can update the table to show that the distance from Cave A to Cave A is 0.

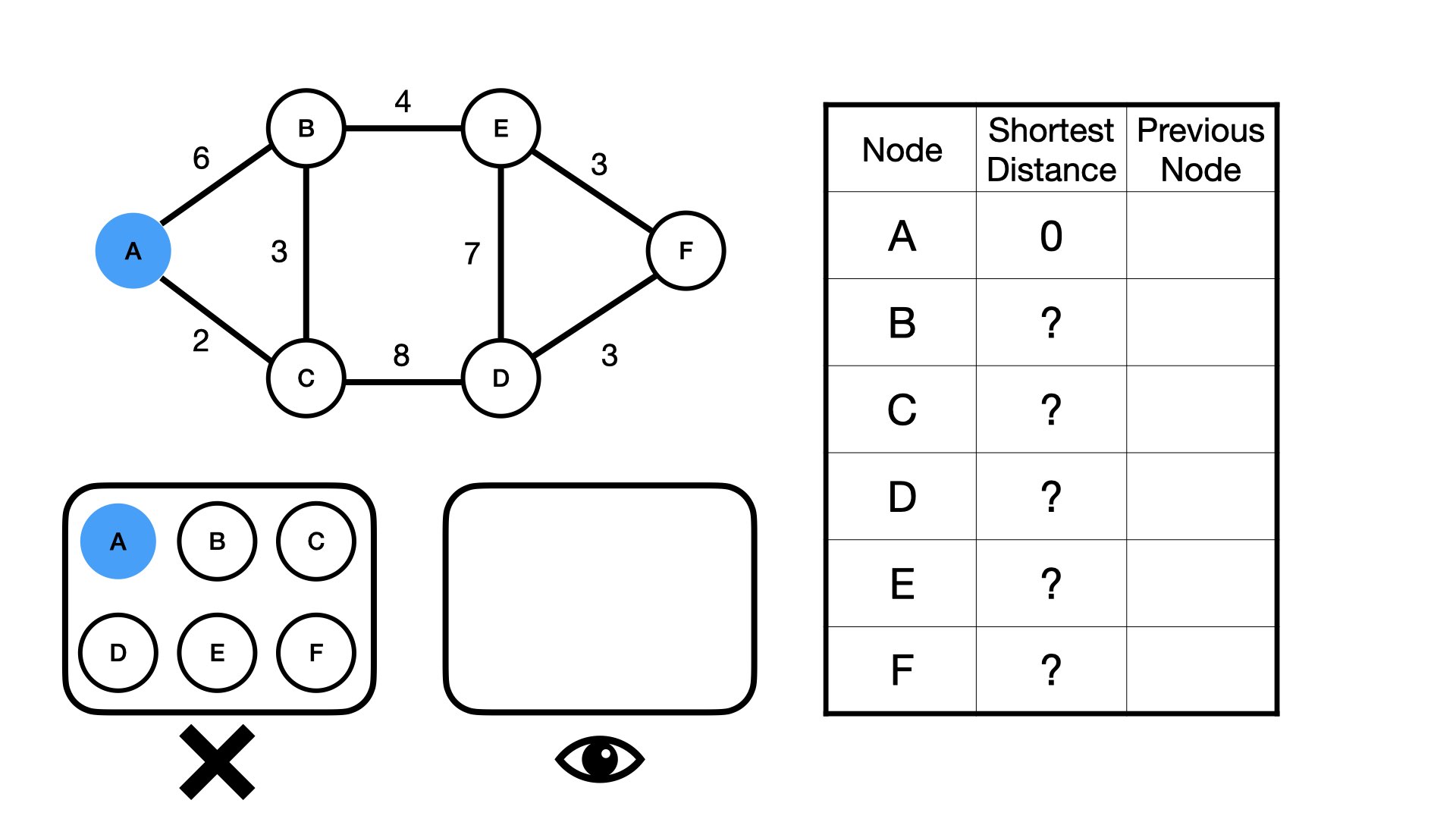
Now we need to calculate this distance between Cave A and all unvisited neighbors of A, which in this case is Cave B and Cave C.

So what do we mean by unvisited here? A cave can be considered as visited when we know the shortest distance between Cave A, the given cave, and all its neighboring caves.

Because we calculated the distance between "A" and all its neighboring nodes, we can call A visited.

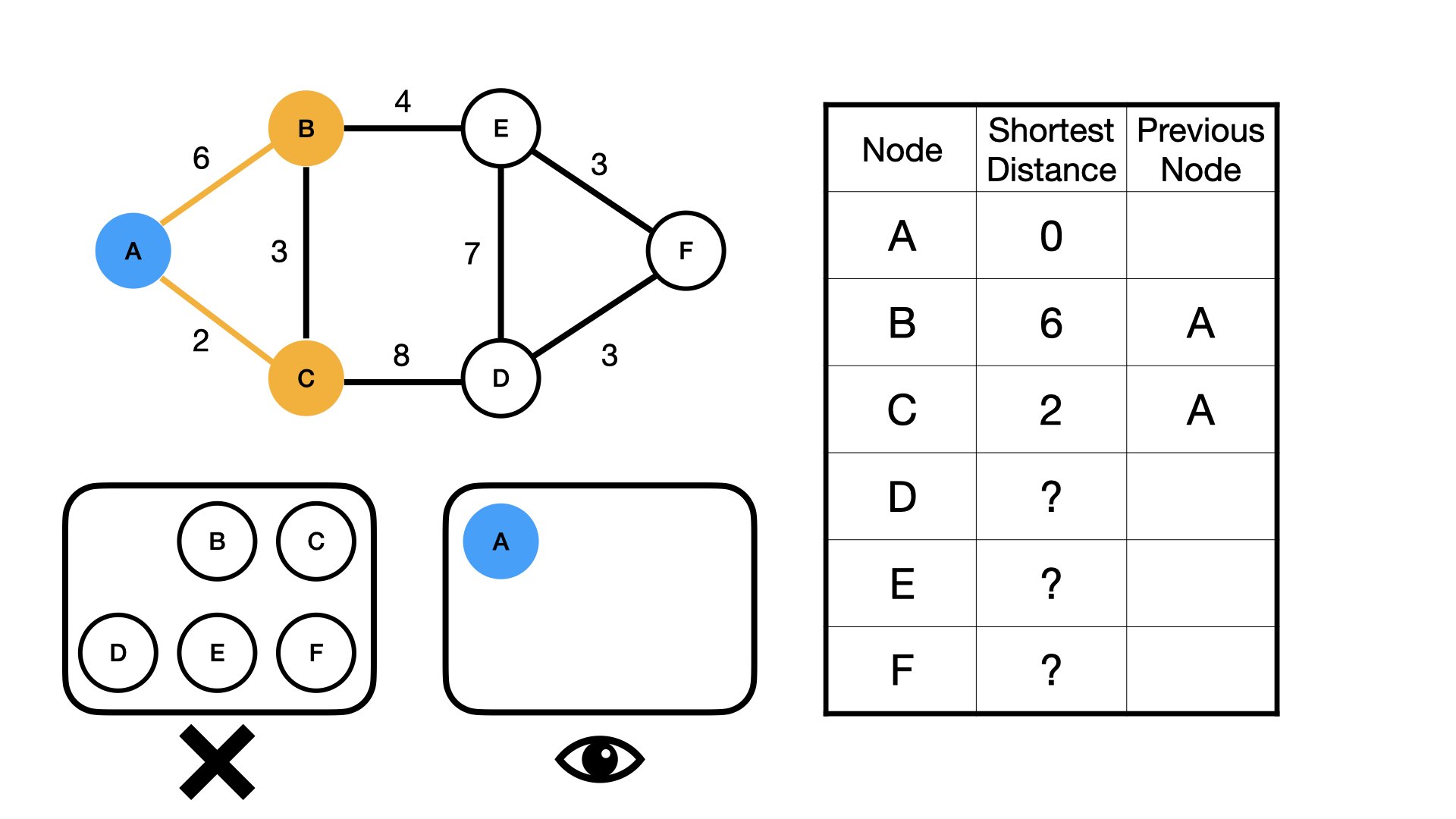
The second iteration

Here comes the genius of the algorithm. Next we choose the neighboring unvisited cave with the shortest distance, which in this case is C, to be our cave of interest.

We repeat the process here. We now calculate the difference between C and all unvisited caves of C:

• "A" is visited at this point (we know the distance to all its neighboring nodes)
• "D" has not been explored at all at this point, so it definitely counts as unvisited
• "B" has been explored, but we do not yet know the distance to all its neighboring nodes, so it is considered unvisited.

Now we update the table. Let's focus in on B. The current shortest distance between A and B is 6. But by going through C, the newest shortest distance will be 5, so we will update the table.

We also update the distance for D to be 10.

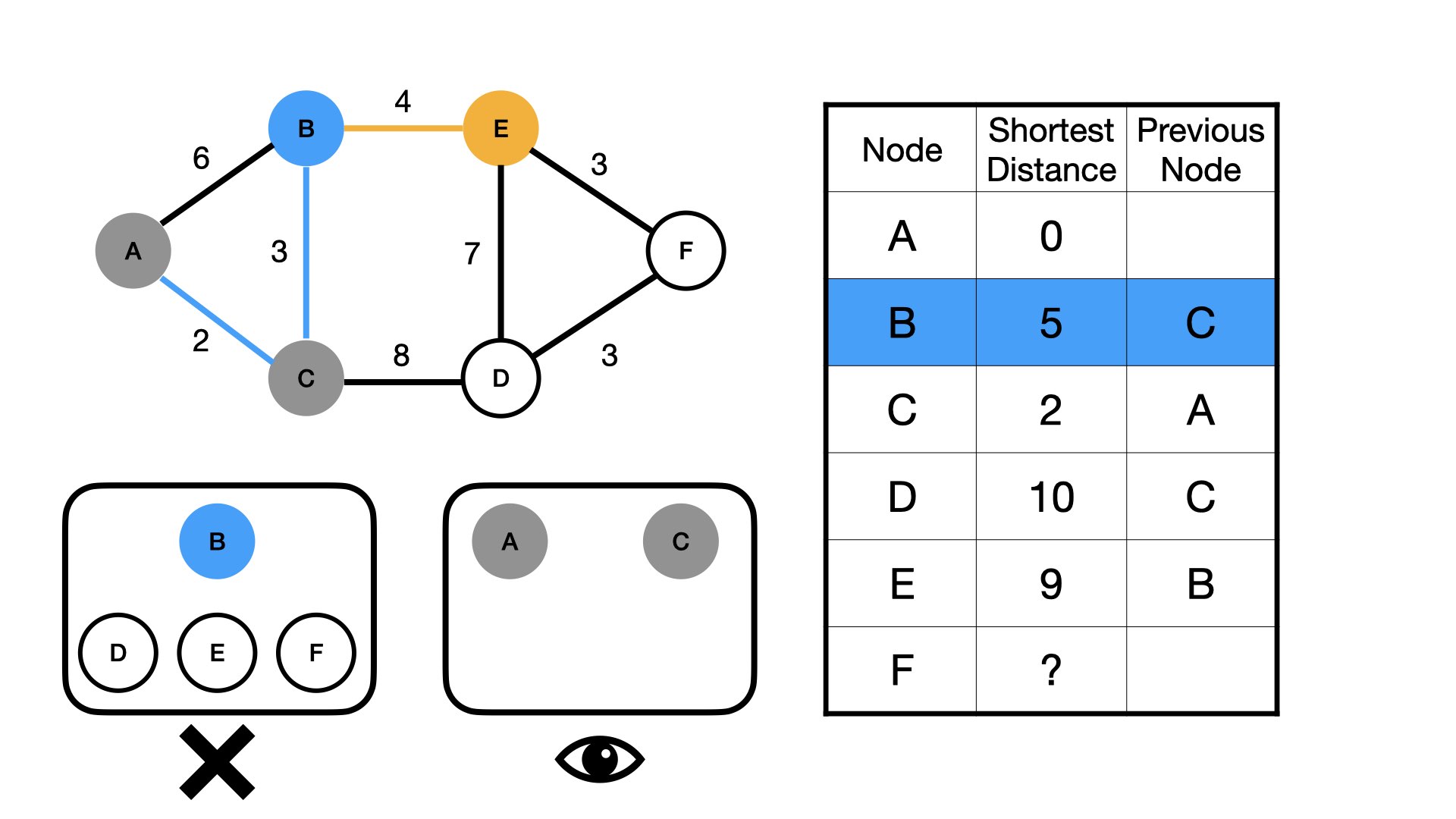
Ok so now we are finished with C because we have measured all previously unvisited nodes of C.

We then choose the nodes from C's unvisited neighbors with the shortest distance which in this case is B, as 5 is less than 10.

The third and fourth iteration

B only has one unvisited neighbor— "E". It takes a length of 9 to reach E, so we update the table. We now mark B as visited and make E our node of observation.

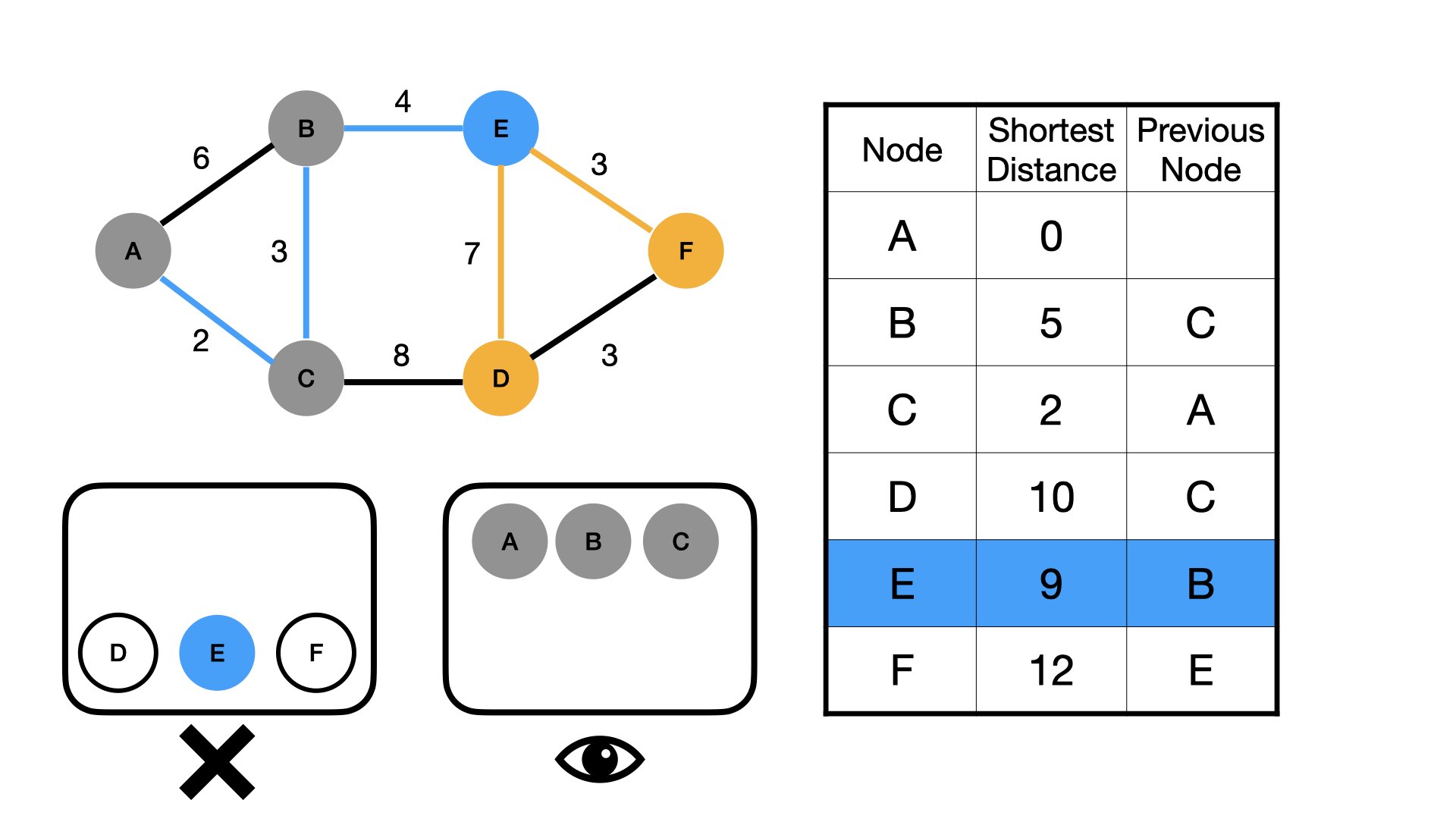
E has two unvisited neighbors— D and F. The quickest path to D through E would be 16 compared to just 10 when going through C, and F's would be 12. We can now mark E as visited.

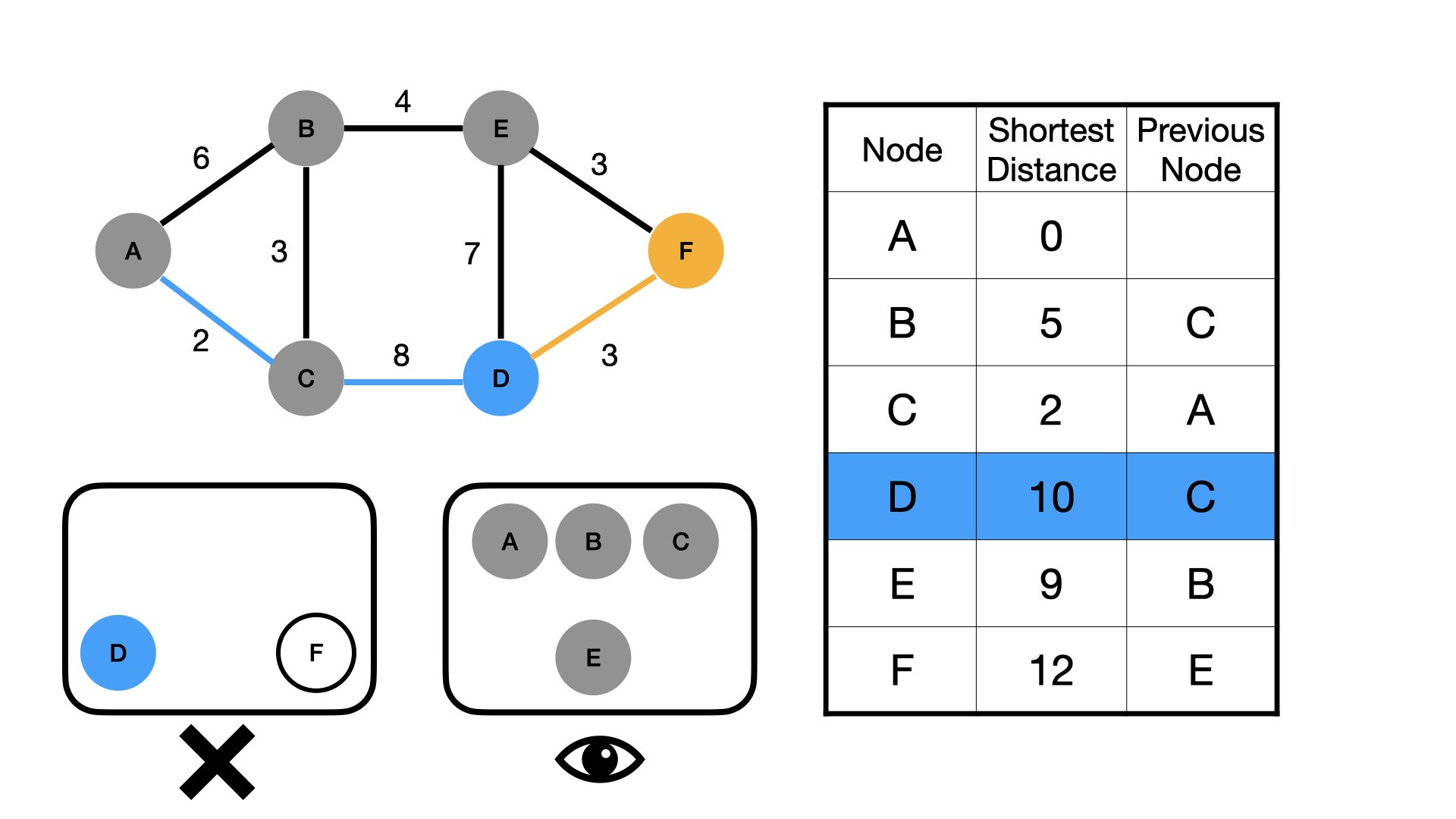
Look at our table. At this point, D has the shortest distance of our unvisited neighbors, even though we are off what had previously been the "shortest path".

D has only one unvisited neighbor— "F". Our previous shortest distance to D was 10, so the shortest path through D to F would be 13, which — devastatingly — is longer than the path through E.

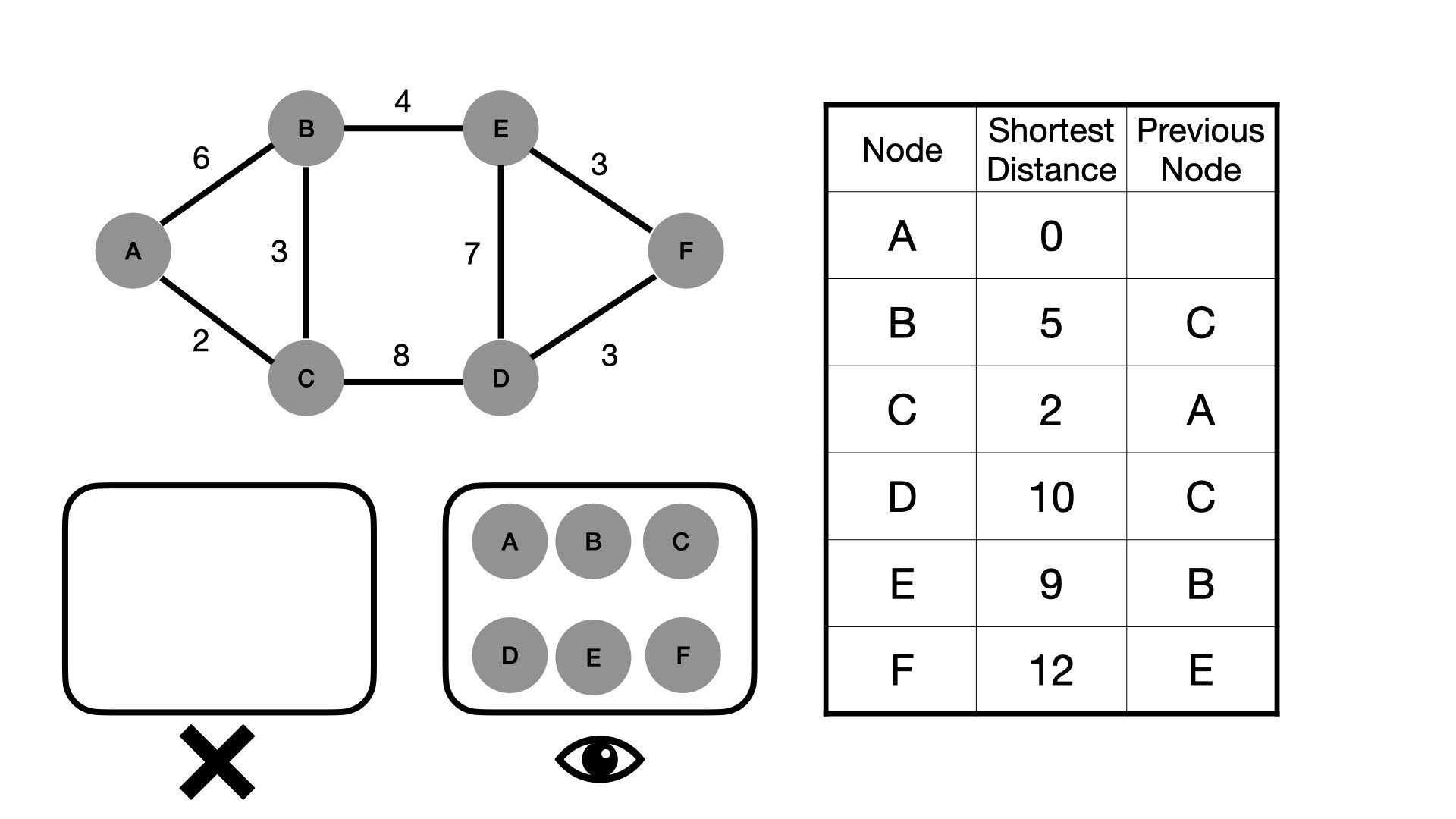
Now What?

Our table shows us the shortest possible distance between Cave A and everything other cave. Our previous node gives us a clue to what path we would need to take.

Its 12 tunnel units (or whatever) from Cave A to Cave F. The previous node is was Cave E. It's previous was B, and so on all the way back to A.