Connected Components

Consider the below graph. We can easily see that there is likely to be two natural groupings here. Amazingly, they are already color coded into their two groups. So how might we formalize our intuition here?

For once, it's actually painfully simple.

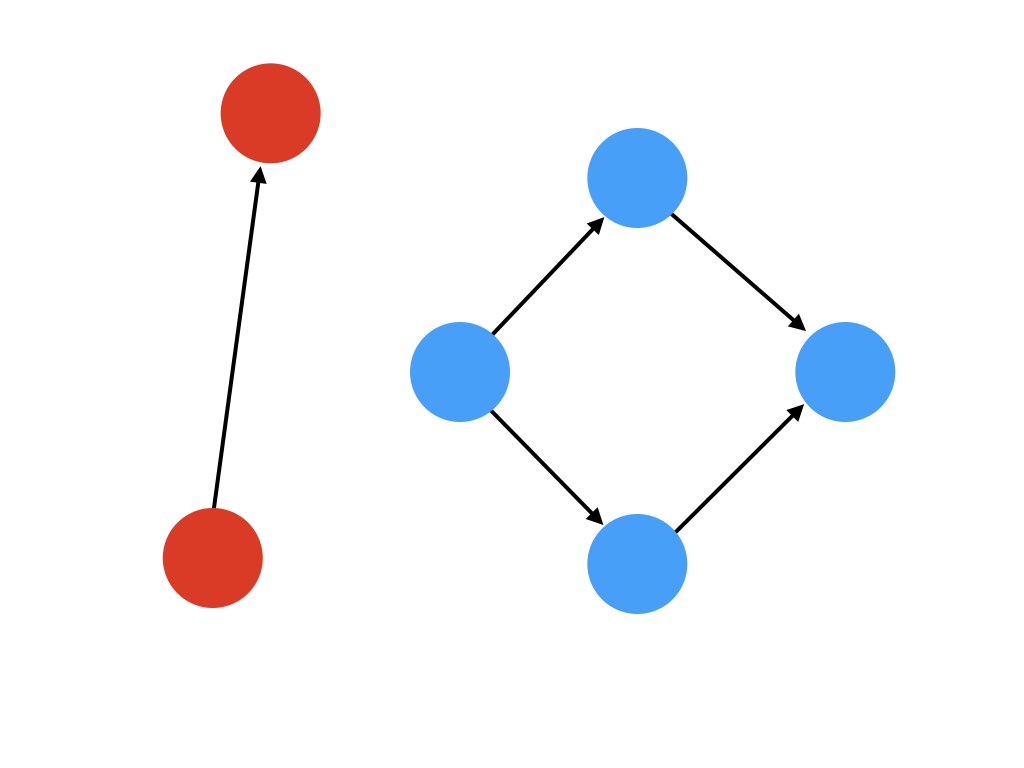
Weakly Connected Components

You might want to do a simple breadth first search to simply see what nodes are reachable for any other node. However, take the left most node in the blue group. That node only has outward bound relationships. It is unreachable from the other nodes, and thus wouldn't be included in a breadth first search from the other nodes. The same issue exists for our red pair of nodes.

Instead, we see what groupings would turn up if we had only undirected or two way relationships between all the nodes.

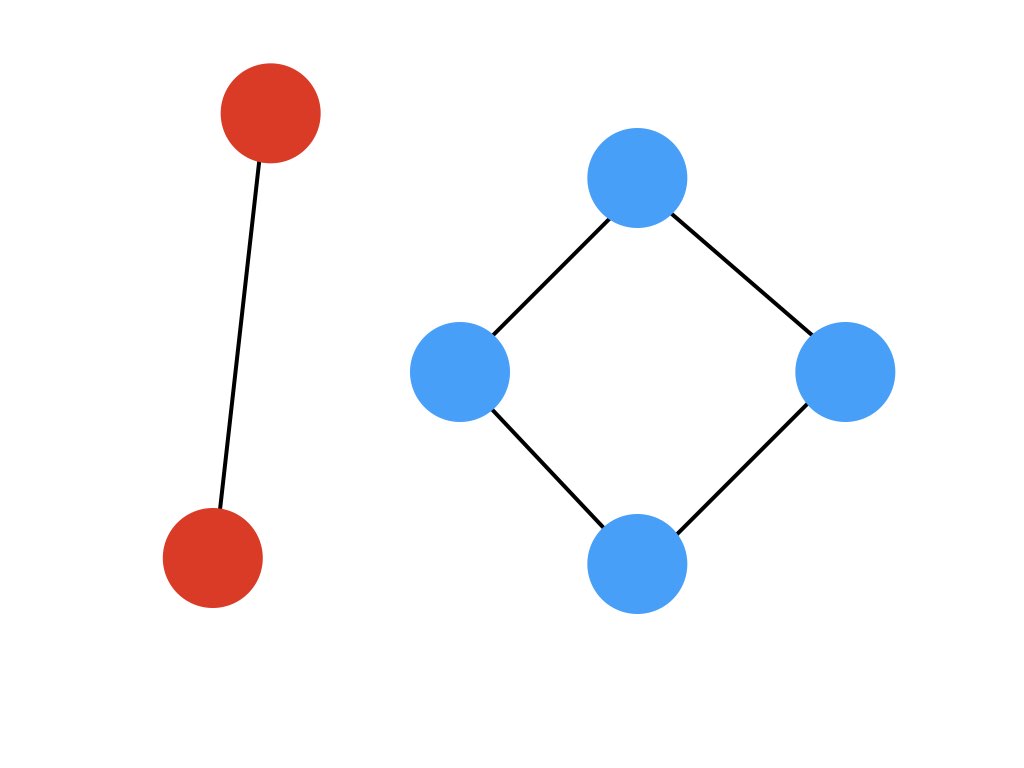
If we ran a breadth first search here on each given node, and assigned each node a component id based on if they were reachable, then we would find two components— just like we were hoping to!

These two groupings are considered weakly connected because they are only reachable to each other with undirected relationships.

Strongly Connected Components

You will likely be able to guess where I am going with this. BUT, strongly connected components are when any node in a component has a path to any other node in that component using the existing directed relationships. Basically, you need some sort of circular path within your connected components.

So what does that look like?

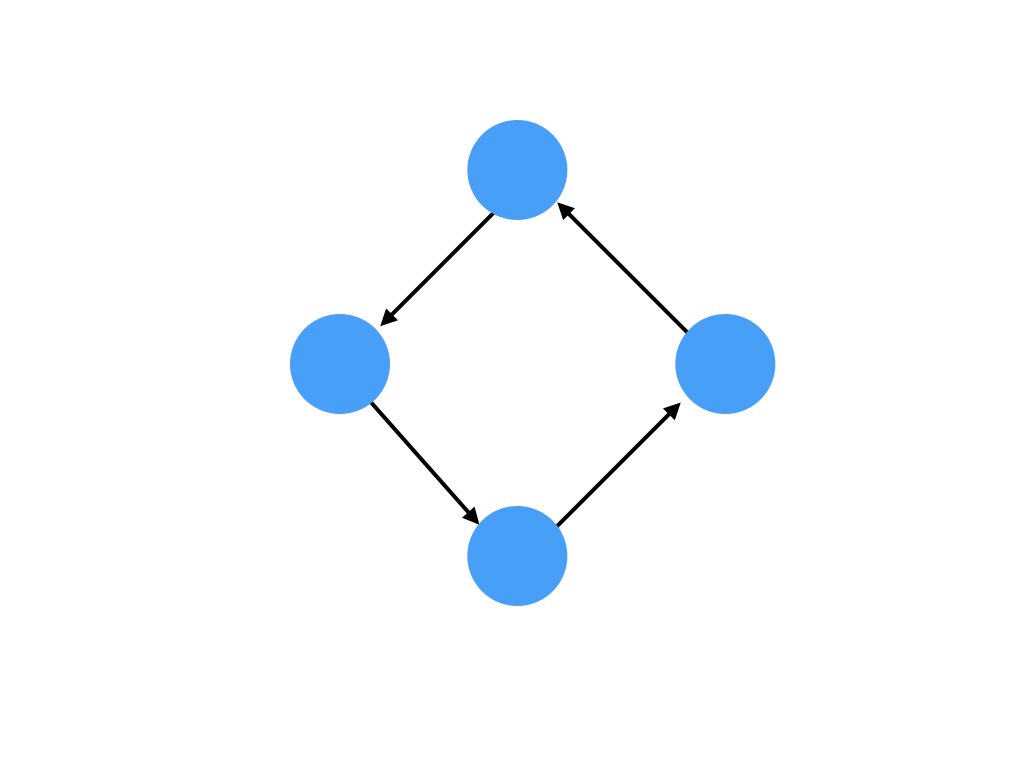
You can trace a path from any node in this graph to any other node just following the relationships. This has some interesting use cases in fraud and money laundering, as you can identify circular payments!