Basic Centrality Measures
Conceptually— what node is the most central in a graph is a somewhat intuitive concept. But on second glance, there might be a little more to that question than first appears.
Do we simply mean what node has the most connections in a graph? Do we mean what node is most important for the flow of information and goods through a graph? Do we mean what node is closest to all the other nodes, even if its not the most connected?
At its core, centrality is measuring the importance of a given node.
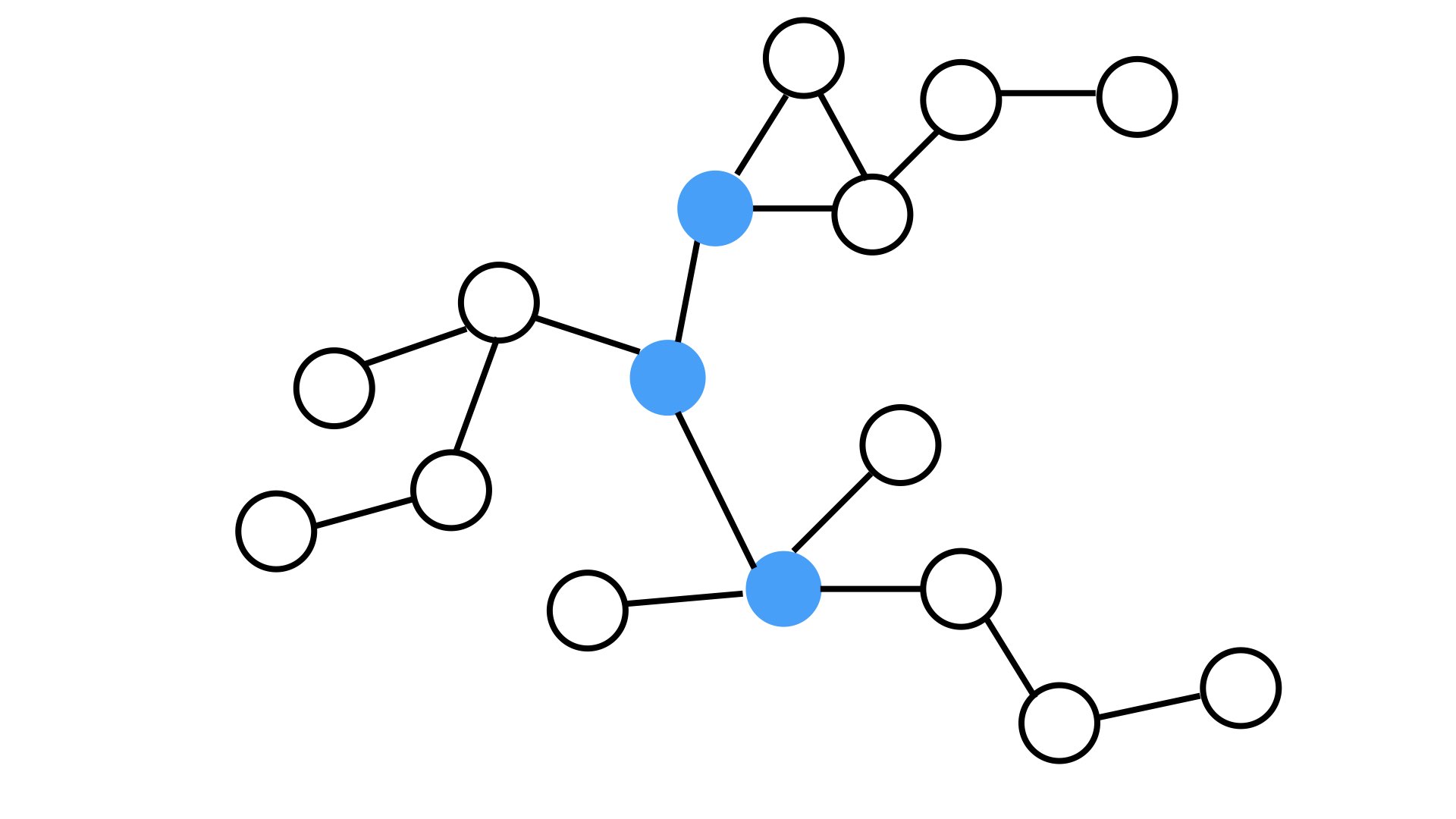
Degree Centrality
Degree centrality is the most straightforward measure of centrality in the graph. It simply assigns an importance score based on the number of links held by each node.
Let's imagine we have a graph of office workers. Each relationship represents office workers who know each other. If we use degree centrality, we would simply be saying that the office worker who knows the most colleagues is the most important in the graph.
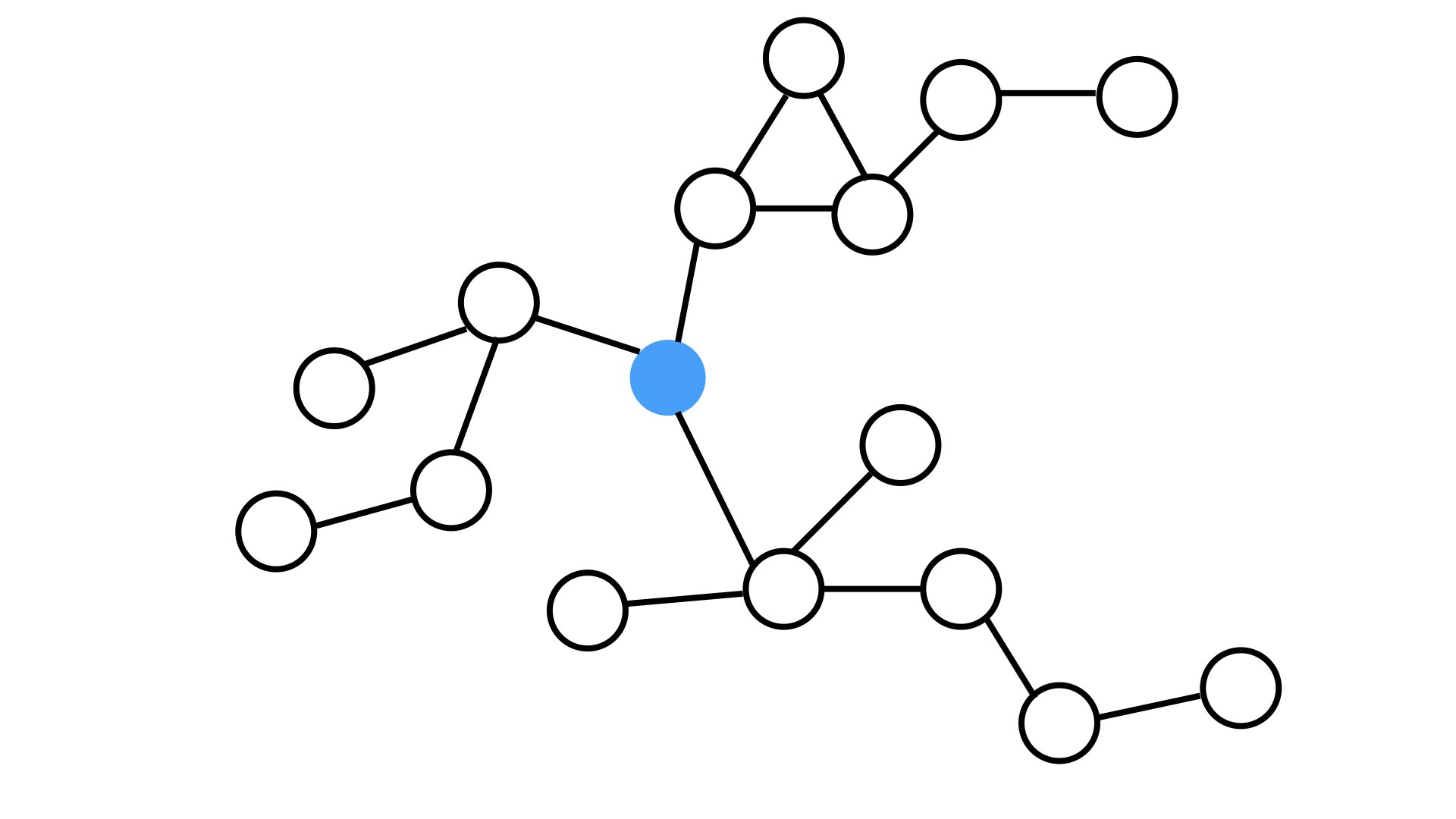
Betweenness Centrality
Degree centrality might be useful in determing the most popular office worker but perhaps not the most important. Who best controls the flow of information? Someone might be really popular among the accountants but has no idea what is happening with the salespeople.
Betweeness centrality measures the number of times a node lies on the shortest path between other nodes.
So we might use something like Dijkstra's algorithm or a breadth-first search to determine the shortest paths and then see which node is most commonly on a shortest path.
Look at our graph, we can see how our new most central node no longer the node with the most relationships but the node that sits between different groups of nodes.
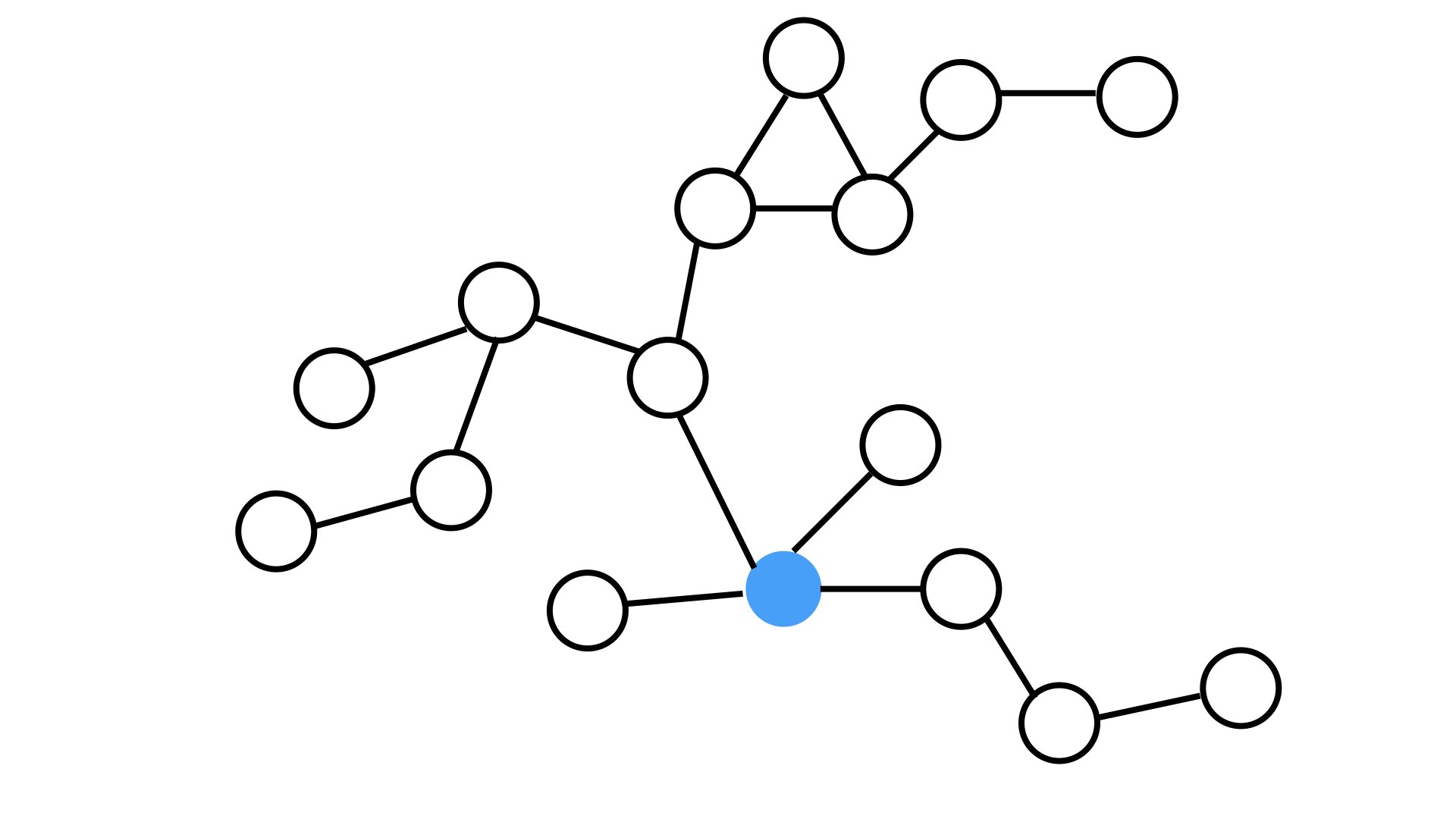
Closeness Centrality
Closeness centrality does something similar to betweeness centrality. Instead this time, we are focusing on how quickly a node can get to all other nodes in a graph.
Here's how we calculate it.
- For each node, find the shortest path to every other node
- Sum up all the lengths of these paths
- Take the reciprocal to get the closeness centrailty
In our office example, we might have a few nodes with similar degrees of closness centrality. This is because its not about being on the shortest path the most but simply being closest to the most nodes. So our very between node is only one hop from three nodes but isnt particularly close to the nodes farther on the edges.